作者：罗春财
　　顾客满意度模型是一个多方程的因果关系系统——结构方程模型（SEM，Structural Equation Model），有多个因变量，是一个原因和结果关系的网，模型必须要按照这些关系进行估计。模型中包括质量感知、顾客满意度、顾客忠诚度和企业形象等隐变量，这些隐变量只能通过多个具体测量变量来间接衡量。模型中允许自变量和因变量含有测量误差，还必须要计算出来隐变量的表现得分（例如通过多个测量变量的加权指数）。
　　以ACSI模型为例，它就是一个结构方程模型，包括结构方程（隐变量之间关系的方程）和测量方程（隐变量和测量变量之间关系的方程） 。要对结构方程模型进行参数估计，目前最经常使用的两种方法是PLS（Partial Least Square）方法和LISREL（LInear Structural RELationships）方法。这两种方法既有相同之处，也有许多不同之处。本文主要讨论两种方法的算法，以及他们之间的联系与区别，并根据实证案例，提出我国在构建顾客满意度模型过程中使用的方法。
　　一、PLS和LISREL方法
　　PLS（Wald，1982）是将主成分分析与多元回归结合起来的迭代估计，是一种因果建模的方法。瑞典、美国和欧盟模型都使用这种方法进行估计。在ACSI模型估计中 ，该方法对不同隐变量的测量变量子集抽取主成分，放在回归模型系统中使用，然后调整主成分权数，以最大化模型的预测能力。PLS方法的具体步骤如下所示。
　　步骤1：用迭代方法估计权重和隐变量得分。从④开始，重复①—④直至收敛。

　　步骤2：估计路径系数和载荷系数。
　　步骤3：估计位置参数。
　　PLS方法是“偏”LS，因为估计的每一步都在给定其他参数条件下，对某个参数子集的残差方差进行最小化。虽然在收敛的极限，所有残差方差联合的进行最小化，但PLS方法仍然是“偏”LS，因为没有对总体残差方差或其他总体最优标准严格的进行最小化。
　　LISREL（Joreskog，1970）方法通过拟合模型估计协方差 与样本协方差（S）来估计模型参数，也称为协方差建模方法。具体来说，就是使用极大似然（Maximum Likelihood，ML）、非加权最小二乘（Unweighted Least Squares，ULS）、广义最小二乘（Generalized LeastSquares，GLS）或其他方法 ，构造一个模型估计协方差与样本协方差的拟合函数，然后通过迭代方法，得到使拟合函数值最优的参数估计。例如，采用ML方法的拟合函数的形式为：
　　LISREL中的步骤与PLS相反：先估计参数，然后如果需要，再考虑所有结构信息，对所有观测变量作回归，“估计”隐变量。LISREL 软件可以进行模型的识别，对所有估计参数的标准误进行检验，并对模型拟合程度进行检验。
　　为了得到最优估计，ML方法的计算量很大。最麻烦的是信息矩阵（也称为Hessian矩阵，即似然函数对模型中任意两个参数的二阶偏微分矩阵）。如果模型可识别，Hessian矩阵必须是正定的。
　　二、两种方法的联系与区别
　　上面简要介绍的PLS和LISREL方法，既有相似之处，也有不同。它们的第一个相似点是都采用箭头示意图作为模型的图形表示。第二个相似点是在每个区组（block），都假设测量变量与隐变量和误差项为线性关系，即y=Λyη+ε x=Λxξ+δ （6）
　　第三个相似点是路径关系（PLS中称为内部关系）的表达形式一样，η＝Βη+Гξ+ζ 或 （I-Β）η＝Гξ+ζ。 （7）
　　第四个相似点是对每个内生变量区组，都给出显变量y的因果－预测关系，即用隐变量路径关系中的解释变量来表示y，y=Λy（Βη+Гξ）＋ε＋Λyζ （8）
　　PLS和LISREL也有许多不同之处。它们的区别类似主成分分析与因子分析的区别。PLS是从主成分分析发展而来的，LISREL是从因子分析发展而来的。
　　第一，分布假设不同。PLS为了处理缺乏理论知识的复杂问题，采取“软”方法，避免LISREL模型严格的“硬”假设。这样，不论模型大小，PLS方法都可以得到“瞬时估计（instant estimation）”，并得到渐进正确的估计，即PLS方法没有分布要求，而LISREL方法假设显变量的联合分布为多元正态。
　　第二，目标不同。PLS方法的目标是根据区组结构（6）、内部关系（7）和因果预测关系（8）进行预测，而LISREL方法研究的目标是矩阵Σ的结构。
　　第三，准确性取向不同。PLS估计在样本量很大和每个隐变量的显变量很多时，是一致（consistency）和基本一致（consistency at large）的，但LISREL估计在大样本时是最优的（置信区间渐近最小）。最优性包括一致性，但一致性不包括最优性。因此，PLS和LISREL对同一参数的估计都在一致性的范围内。两种估计的差别不可能、也不应该很大。
　　第四，假设检验不同。PLS方法采用Stone（1974）和Geisser（1974）的交互验证（cross-validation）方法检验，考察因果预测关系（8）。LISREL方法一般使用似然比检验，考察观测矩阵S和理论矩阵Σ的拟合程度。
　　第五，估计顺序不同。PLS方法通过逼近，先将每个区组的隐变量的估计得分表示为测量变量的加权合计， ，然后通过一系列权重关系的迭代，得到权重的估计。LISREL方法先估计载荷Λy和Λx，在这个过程中消去隐变量，然后通过对测量变量的多元OLS回归，估计隐变量的样本值（因子得分）。
　　第六，对方程中变量间的关系理解不同。PLS方法将系统部分（6）和（7）定义为给定解释变量值时的条件期望，作为变量间的因果预测关系。因此，对于（6），PLS方法假设，
　　E（y/η）=Λyη E（x/ξ）=Λxξ （9）
　　对于（7），PLS方法假设，
　　E（η/η，ξ）＝Bη+Гξ （10）
　　而LISREL方法将结构关系（6）和（7）定义为具有误差的确定性“方程”，即变量间是具有误差的确定性关系。
　　第七，模型的识别不同。PLS方法中，虽然隐变量的估计是逼近得到的，但由于估计是显式的（explicit），因此PLS方法中没有识别问题。LISREL方法中，矩阵Σ的结构是由区组结构（6）决定的，（6）又受到路径关系（7）的限制，LISREL方法有可能不能识别模型。因此，LISREL估计的第一个阶段就是考察模型的可识别性。如果不能识别，模型中必须包括一些参数假设（reparameterization assumption）。
　　最后，PLS方法中，还可以选择三种加权关系，取决于更关注（6）、（7）还是（8）的操作性。权重关系模式A和模式B分别使用简单OLS回归和多元OLS回归，模式C是二者的结合。在PLS模型的图形中，显变量与其隐变量之间的箭头指向表明了选择的估计模式。
　　三、PLS和LISREL的适用条件
　　人们在两种方法的选择上一直存在分歧，由以上比较可见，PLS适用于以下情况：
　　1．研究者更加关注通过测量变量对隐变量的预测，胜于关注满意度模型的参数估计值大小，因为PLS的估计量是有偏的，但可以根据测量变量得到隐变量的最优预测 。
　　2．适用于数据有偏分布的情况，因为PLS使用非参数推断方法（例如Jackknife），不需要对数据进行严格假定；而LISREL假设观测是独立的，且服从多元正态分布。
　　3．适用于关注隐变量得分的情况，因为PLS在参数估计过程中就计算隐变量得分，可以得到确定的计算结果。而LISREL在进行参数估计之后，再采用某个目标函数计算隐变量得分，计算结果因目标函数选择不同而不同。
　　4．适用于小样本满意度研究 ，因为PLS是一种有限信息估计方法，所需要的样本量比完全信息估计方法LISREL小得多。
　　5． 适用于较大、较复杂的结构方程模型，因为PLS收敛速度非常快，计算效率比LISREL更高 。但对于不太复杂的顾客满意度模型，计算时间的优势不明显。
　　LISREL适用的情况不同：
　　1．研究者更加关注满意度模型的参数估计值大小，即测量变量对隐变量的影响和测量变量的效度，而不是纯粹的预测应用；而且，只有当模型的参数估计无偏时，才能验证测量变量的效度，因此PLS不能对此进行验证，因为PLS估计的隐变量路径系数有低估，不能揭示隐变量之间的关系（Dijkstra, 1983）；PLS的隐变量载荷的参数估计易于趋同，且有高估偏差。
　　2．适用于不同的样本间参数估计比较的情况，因为LISREL可以提供 检验，而PLS得到的权重、载荷和隐变量得分在不同样本间的可比较性是一个值得怀疑的问题。
　　同时，随着LISREL的发展和完善，也可以利用PLS的思想来弥补自身的缺陷：
　　3．尽管LISREL中ML估计的有效性、标准误差和检验统计量的正确性需要数据正态和独立的假设，但只要满足某些条件，这些特性并不会受到非正态的影响（Satorra,1990）。此外，LISREL也可以像PLS一样使用非参数重抽样方法（例如bootstrap）进行统计推断。
　　4．LISREL中的ML估计，即使分布假设不成立也非常稳健，可以得到总体参数的一致估计。然后基于这些参数，采用几种目标函数计算隐变量得分。这些目标函数不同于PLS目标函数，但这并不能说明得分是不确定的。而PLS通过最大化测量变量的可靠性估计和隐变量回归的R2来计算隐变量得分，导致PLS参数估计有偏 ，使隐变量得分的价值大打折扣。
　　实际上，两种方法各有千秋，分别适用于不同的情况。从根本上说，由于算法的不同，PLS对测量变量协方差矩阵的对角元素的拟合较好，适用于对数据点的分析，预测的准确程度较高；LISREL对测量变量协方差矩阵的非对角元素的拟合较好，适用于对协方差结构的分析，参数估计更加准确。两种方法的选择取决于研究的目的。当研究目的是理论检验且先验理论知识充足时，更宜采用LISREL；当研究目的是因果预测应用，且理论知识非常缺乏时，则PLS更加适合。因此，从实用的角度可以说，ML和PLS方法是互补的，而不是互斥的。
　　四、我国构建顾客满意度模型时估计方法的选择
　　对于我国顾客满意度模型估计方法的选择，主要应该在我国不同行业的不同公司进行试算，也可以采取模拟数据进行研究，参照国外的研究结果，对我国的实证结论进行PLS和LISREL的比较。
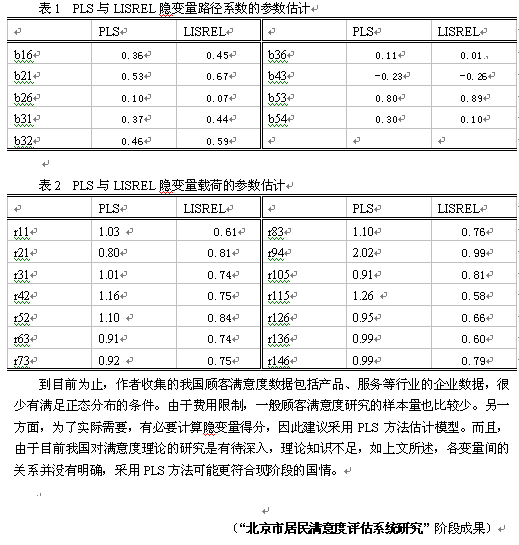
　　作者对某服务行业公司的满意度数据进行测算 ，两种方法得到的结果进行比较，结论与前文类似。PLS估计的隐变量路径系数有低估，PLS的隐变量载荷的参数估计易于趋同，且有高估偏差，结果如下表所示 ：

　　作者介绍：河南君友商务咨询有限公司行业研究部经理